場合の数と確率の分野では、原則として「人」は何も書いていない場合は区別します。 一人一人が3つの部屋の内から行きたい部屋を選ぶと考えて、3 6 =729(通り)// 例題(12)同条件で空室があってはならないとする。 この場合は(11)の総数から (α)全員が1つの部屋へ行く 3通り (β)全員女性3人、男性4人の7人のサークルで、卒業記念写真を撮ることになった。横一列になって撮る時、必ず女性3人が真ん中になるようにする撮り方は何通りになるか。 A:24通り B:48通り C:60通り D:96通り E:1通り F:144通り G:160通り H:192通り5枚のコインの出方って何通りありますか?? 0 回答 ベストアンサー シロクマ 約3年前 1枚が2通り、2枚なら4通り、3枚なら8通り、4枚なら16通り、5枚なら32通りです。 すなわち、n枚のコインの出方は2のn乗なのです。 0 ( ॑꒳ ॑ ) 約3年前 わかりました!ありがとうございます┏ 1 こ

組み合わせは何通りもあるので飽きずに遊べます 大木のおもちゃ動物
組み合わせ 何通り
組み合わせ 何通り-組み合わせには、次の性質があります。 組み合わせの性質 これは、 個の中から 個を選ぶことが、 選ばない 個を決めることと同じ になるからです。 選び出す数 が大きいとき にこの性質を使うと計算を楽にできるので、ぜひ活用してみてくださいね。 (例) → → 組み合わせの計算方法例題 例題を通して、組み合わせの計算方法を確認しましょう。 例題 A、B、C、D、E の 人の中から= 24 通りあります。 つまり、 A = 1 、 B = 2 、 C = 3 、 D = 4 での組合せの数を調べ、 24 倍するとすべての組合せの数になります。 これで、処理時間を24分の1に短縮できます。 ソースコード A = 1 、 B = 2 、 C = 3 、 D = 4 とした場合の組合せの数




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
トッピングを組み合わせると1億通りにもなるというカレーチェーン カレーハウスCoCo壱番屋 。 1億通りにどれくらい近づけるか、食べた記録を残しておきたいと思います。 目次 カレーチェーンといえばやっぱりCoCo壱番屋(ココイチ) ココイチのトッピングリスト 肉類のカレー 手仕込ヒレカツカレー300グラム&半熟タマゴタルタルソース 手仕込ヒレカツ組み合わせの求め方を理解するには、順列の理解が不可欠なので、これについてもおさらいしておくことにしましょう。 2 順列と組み合わせの違い 上で見た通り、組み合わせでは要素の並び方は考慮に入れません。つまり、「並べ方が違っても要素が同じ右の図のように、道路が碁盤の目のようになった街がある。地点 a から地点 b までの長さが最短の道を行くとき、次の場合は何通りの道順があるか。(東北大)(1) 地点 c を通る。(2) 地点 p は通らない。(3) 地点 p 、および地点
複数リストから全ての組み合わせデータを作りたい(1/2) データ 今回は、いくつかの項目リストをもとに、その組み合わせの全パターンデータを、Excel を使って作成する手順について調べます。 また、それを自動生成するマクロを作成します。 長くなったので記事を2回に分けます。 今回は Excel 10 と 13 に対応した手順です。(c, c, c) の 4通り。 合計で、64 で 10通りになりますね。 この分け方は、小学校で習った「樹形図」や「辞書式」の考え方です。 no1 さんの挙げたサイトの他に、次のサイトも参考になるかも。ということで、まずは、以下の図の条件を満たすABCDの組合せが何通りあるかを調べます。 ABCD と 1234 を対応付ける組合せは、 4!
よって24通りです。 例題 (組み合わせ) 次の組み合わせは何通りか。 ①7人から3人を選ぶ選び方 男子5人、女子2人の中から男子2人、女子1人を選ぶ選び方 解答 ①\(_7 C_3 =\frac{7⋅6⋅5}{3⋅2⋅1}=35\) よって35通りです。Coin = 2, 3, 5 total = 14 def combinations(coin, total) dp = int(i % coins0 == 0) for i in range(total 1) for coin in coin1 for i in range(coin, total1) dpi =5個のボールの並べ方は何通りあるか WolframAlpha WolframAlphaのご利用についてのご質問は Proプレミアムのエキスパートサポートまで お問い合せください »




小6算数 ならべ方と組み合わせ方 学習プリント 練習問題 無料ダウンロード印刷




組み合わせは何通りもあるので飽きずに遊べます 大木のおもちゃ動物
組み合わせを全通り表示 組み合わせを全通り表示するには、 「combinations ()」 を使用します。 combinations (配列, k) ここで、nは配列の要素数になります。 以下のプログラムは、n=5、k=2の場合の組み合わせを全通り表示するプログラムです。 import itertools com = 1, 2, 3, 4, 5 com_list = list(itertoolscombinations(com, 2)) print(com_list) 解説 com_list = list( 1) ( 1) n k n nPk n n n k u u u基本的には上述の何通りかの組み合わせの計算方法と同じです。ただ、使える数字が1~9と9種類に変化していることから、9×9×9= 729通りと計算できることになります。 パスワードではない3桁の数字は何通りあるか? このようにパスワードなどでは先頭行を0とした0xxなども組み合わせの一つと




1日1題spi 順列 組み合わせ サプログ 企業の人事 大学の教授 職員 社会人 内定者との協力体制を整え 就活生 そして働くことを頑張りたい人を応援します




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ
について解説していきます。 重複を許す組み合わせとは次のような問題のことですね。 りんご,みかん,バナナの3種類から重複を許して,4個取り出す組み合わせは全部で何通りあるか。 まずは、こちらの問題をどのような考え方で解けばよいのか解説A が2個の場合: (a, a, b);続いて4人の中から3人を選ぶ場合の組み合わせが何通りあるのかについても確認していきます。 こちらもnCrの公式を活用しますと、4C3=4C1=4通りと求めることができます。 この意味についても詳しく解説します。 まず4人の中から3に選ぶ際に、残りの1人も自動的に決まるところに着目



トランプの並びは何通り 新しい組み合わせができる確率は 数学の面白いこと 役に立つことをまとめたサイト




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
組み合わせは何通り? ・アルバイトのシフト組み合わせパターン計算 ・カードゲームのデッキ組み合わせパターン計算 Read more Collapse Reviews Review policy and info Loading What's New ターゲットSDKをAPIレベル29(Android10)に変更 Read more Collapse Additional Information Updated Size M Installs(a, a, c) の2通り。 a が3個の場合: (a, a, a) の1通り、で、a を含む場合は 321=6 で 6通り。 a を含まない場合: (b, b, b);\({}_n C_r = {}_n C_{nr}\)




何通りも組み合わせが楽しめるバングル Happy Plus ハピプラ




キッチンエムズ 組み合わせが何通りもあって楽しめる洋食ランチ 気ままに岐阜をお届けします
競馬ボックス何通り? 計算式 全券種解説 最終更新日: うまめしcom 競馬必勝法の北村です。 ボックス点数早見表 競馬で馬券を買う時にボックス買いの組み合わせ数が何通りかすぐわかるように早見表を作ってみました。 頭数 馬連 馬単 ワイド 三連複 三連単 3頭ボックス 3 6 3 1立候補した5人の中から 図書委員を2名 決める時、何通りが考えられるか。 「0」「1」「2」「3」と書かれた紙がそれぞれ1枚ずつあり、これらから 3枚の紙を選ぶ時 、何通りの選び方があるか。;A、b、c、dの4つのチームで、野球の総当たり戦をします。試合の組み合わせは何通りになるか求めなさい。 解説&答えはこちら 答え 6通り 樹形図で考えると、こんな感じですね。 表を使うなら、こんな感じです。 選ばない!?場合の数 問題 a、b、c、dの4人の中から3人を選ぶとき、選び方
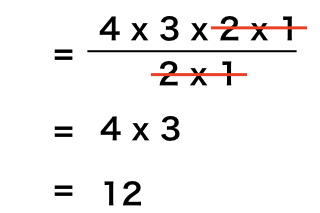



組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather




並べ方と組み合わせ方 その2 家庭学習レシピ
重複組み合わせとは その名の通り、重複オッケーな組み合わせ問題のことです。と説明しても曖昧で分かりづらいと思うので、いきなりですが具体的な問題を例にとって考えていきたいと思います。 問題 りんご、みかん、パインがたくさんある。このたくさんある中から4本当は6通りではなく、この組み合わせを1として数えたいので、 順列に\(r!\)を割ります(※\(\frac{1}{r!}\)) 。 計算すると、 \({}_{10} C_{3} = \frac{10!}{(103)!\times 3!} = 1通り\) となります。 組み合わせは対称性を有する。>今回は、組み合わせパターンを調べる関数をご紹介します。 組み合わせパターンを調べる 例えば、14種類のデータがあったとして、その中から3つを1セットとした場合、全部で何通りのパターンが考えられるか? combin関数での引数の指定 総数:種類の総数



順列と組み合わせを計算する Permut Combin関数 Excel関数




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生
間違いが有ればご指摘頂きたく。 数字の1・2・3を使って (並べて)表すことの出来る数字は 123、132、213、231、312、321の6通りですよね。 この時1・2・2を使うなら、組み合わせは6通りでも 結果として表す事の出来る数の種類は減るので、 表すことの出来る数の種類を求められた場合は 122、212、221の3通りですよね。 同様に1・2・3・4を使うなら24通りで、 1・2・3組み合わせのパターン(combin関数)※反復なし combin関数は『反復なし』の組み合わせを計算します。 上記で説明したとおり、人やチームなど、同じ人や同じチーム同士を除く組み合わせのパターンになります。 例)5人の中から2人を選出する場合: =combin(5,2)ロト6の組み合わせ数は全部で何通り? 数字選択式のロト6は43個の数字の中から6個の数字を選んで、抽選された本数字と合えば1等当選となります。 では、ロト6の組合せ数は全部で何通りあるのか? この計算式は




算数 行き方の組み合わせは何通り 中学受験 全国記述模試1位のプロ講師の個別指導 福岡市早良区藤崎の個別指導塾なら合格get



高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
小学6年生算数で習う 「並べ方と組み合わせ方」「場合の数」の学習プリント (練習問題・テスト・ワークシートドリル) です。 順序よく整理して調べようの単元では、何通りのならべ方や組み合わせ方があるのか、計算や樹形図、表を使いながら学習します。 組み合わせは 確率 の勉強でも使うので中学校入学準備の教材としても使えます。 見落としや重複何通りの方法がありますか? 二人のリーダーを区別することはできません。そのため、組み合わせの問題になります。そこで表を作り、右上半分にチェック( )を加えましょう。 チェックの数が答えになります。 つまり、組み合わせの答えは10通りです。コインの組み合わせは何通り? 〜動的計画法〜 問題:1枚あたりの価値が {2,3,5}の3種類のコインを組み合わせ、金額の合計をちょうど14にするやり方は何通りか。 コインはそれぞれ何枚でも使ってよいとする。 Copied!



2



組み合わせ C とは 公式や計算方法 は何通り 受験辞典
組み合わせは全何通り? 競艇は6艇で競われる競技のため、3連単の組み合わせは全部で1通り。 このことから、3連単が当たる確率は 08%(1/1) となり、的中させることが難しい玄人向けの買い方と言えるでしょう。 確率(的中率)の底上げは可能4桁の数字は何通りある(1~9の場合)暗証番号やパスコードなど 今度は使用する数字が1~9の場合の4桁の数字が何通りとなるのかについて確認していきます。 基本的には上述の何通りかの組み合わせの計算方法と同じです。ただ、使える数字が1~9と9種類に変化していることから、9×9×9×9= 6561通りと計算できることになります。例えば、1, 2, 3の三つの数字について、順列の全ての場合を列挙すると次の6通りがあります。 組み合わせでは、上記6つを全て同じものとみなします。 つまり、順列における並び順のパターンを入れ替えたときに、同じ順番になるものはそれを1通りとみなさず、1, 2, 3の三つの数字の組み合わせは、 の1通りのみとなります。 順列 によって並べられた 個の




順列か組み合わせかで解き方が違うと思うんですがイマイチ違いがわかりません た Clearnote




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生
この記事では,「A,B,Cの3文字から全部で7個選ぶ場合の数」のように,同じものがいくつかあってよい「重複組み合わせ」の考え方を説明します. 「重複組合せ」の問題設定としては 選ばれない色のボールがあっても良い場合 選ばれないボールがあってはこの10通りの組み合わせについて、 それぞれ順列を作成し、順次シートに出力しています。 最終的な全順列の数は、 5!= 60 実務での使用場面があるかどうか、若干疑問はありますが、 必要になった時に、いつでも使えるように用意しておくという意味もあります。 同じテーマ「マ




高校生と塾講師 家庭教師 のための数学 数 A 組み合わせ 道順 最短経路 縦3マス横4マスを左下aから右上bまでいく 最短経路は何通り あるか また 縦1横3のポイントcを必ず通過する場合は何通りか




組み合わせは何通り For Android Apk Download
組み合わせか? の判断テクニック では、ここで問題です。 「コインを5回投げたうち、表が2回出るパターンは何通り? 」 この問題では、 順列と組み合わせ、どちらの公式を使うべき でしょうか。 By frankieleon 正解は、 組み合わせの数の公式 。 答えは 5 C 2 =10通りとなります。 この性質から、組み合わせの数は「コインを5回投げたときに2回表が出る 確率 」を求めるときなどにミニロトは全部で何通りあるのかを調べてみたところ、組み合わせは通りでした。 どういう計算でできるのかも解説していきますね。 ミニロトは31個の数字の中から、当たると思われる5つの数字を選ぶものです。 まずは31個から5個を選ぶには何通りかを出しましょう。 31×30×29×28×27で,3,3通り。 一見、,3,3通りもあるの? ! と思ってしまい☆今、大きな話題になっているtoto*BIGですが、 この組合せが全部で何通りあるのか考えてみました。 ホームチームが勝てば1、負ければ2、延長とかそのほかが0です。 つまり1試合に3通り出る確率があります。 対象となる試合数は14試合なので、答えは以外に簡単でした。



1



場合の数
通り 10個の異なる文字(a,b,c,d,e,f,g,h,i,j) を,重複することな く,4個順に並べるときの並べ方は全部で何通りあるか? 10P4 10u9u8u7 通り n 個の異なる文字を,重複することなく,k個順に並べると きの並べ方は全部で何通りあるか? ( )!!教えてください! 数学 4つのもののすべての組み合わせが何通りあるかを教えていただきたいのですが、 ぜんぶなし1パターン 1つを選ぶ4パターン 2つを選ぶ6パターン 3つを選ぶ4パターン 4つ全部選ぶ1パターン よって =16通りでよいのでしょうか? むかし学校で何かを習ったときは、4×3×2=24だったようにも思いましたが、そん




組み合わせ C とは 公式や計算方法 は何通り 受験辞典




小6算数 スクールプレゼンター教材共有サイト スクプレ道場




ビンゴ5の組み合わせ数は全部で何通り 当たる確率や還元率は 宝くじ生活
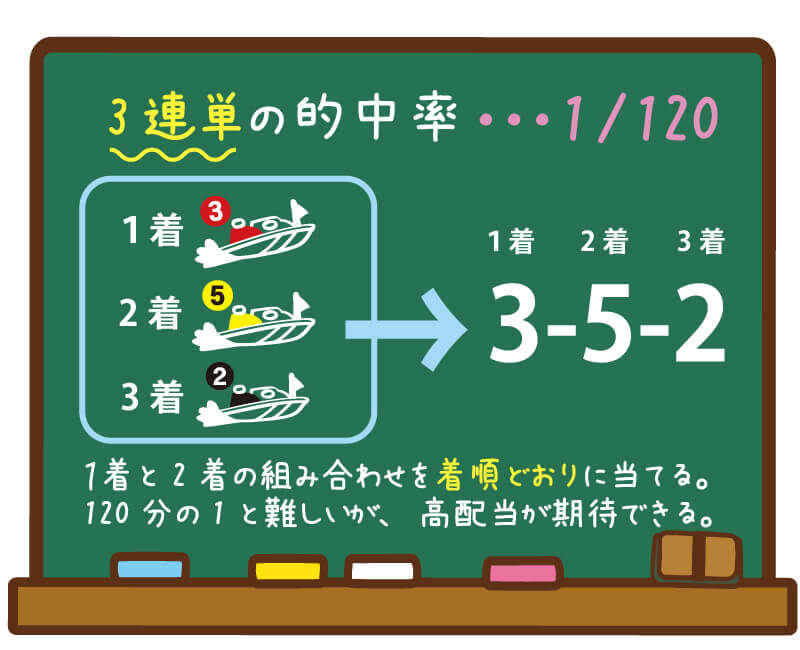



競艇の3連単とは全何通り 当たる確率や平均配当 勝てる買い方を考察 競艇マニア
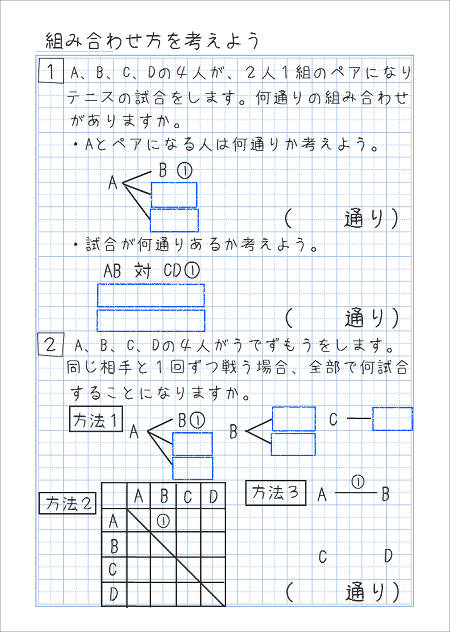



並べ方と組み合わせ方 その1 家庭学習レシピ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




小6算数 場合の数 2 指導アイデア みんなの教育技術



重複順列 Itパスポート出題テーマ別過去問題 平成24年度秋期 テクノロジ系 問78




トランプの並びは何通り 新しい組み合わせができる確率は 数学の面白いこと 役に立つことをまとめたサイト




スマホok 6年 並べ方と組み合わせ方 場合の数 並べ方を考えよう Youtube




組み合わせは何通り For Android Apk Download




4人の中から2人選ぶ場合何通りの組み合わせがあるか 4人から3人選ぶ時は何通りか 5人から3人 4人を選ぶ場合何通りか 確率 モアイライフ More E Life




場合の数 これだけは覚えよう 並べる と 選ぶ の計算方法の違い 中学受験ナビ
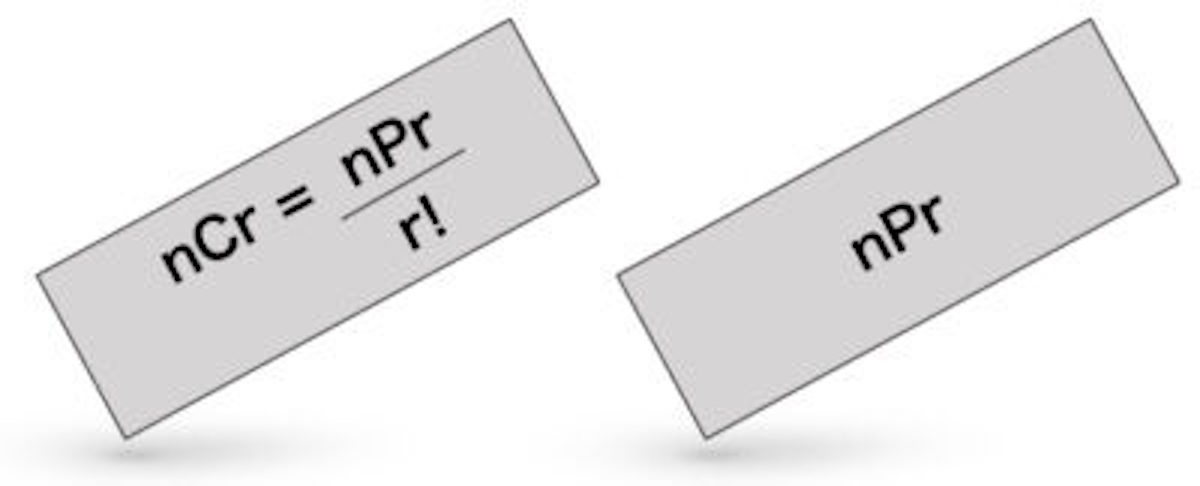



組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ




高校数学 数a 14 組み合わせ 基本編 Youtube




4桁の数字は何通りある 0 9や1 9の場合 6桁の数字は何通り パスワードやパスコードや暗証番号 ウルトラフリーダム




組合せ 数学が嫌いなんです
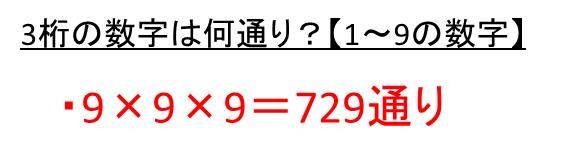



3桁の数字は何通りある 0 9や1 9の場合 5桁の数字は何通り パスワードやパスコードや暗証番号 ウルトラフリーダム




高校数学 数a 16 組合せ 男女編 Youtube




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



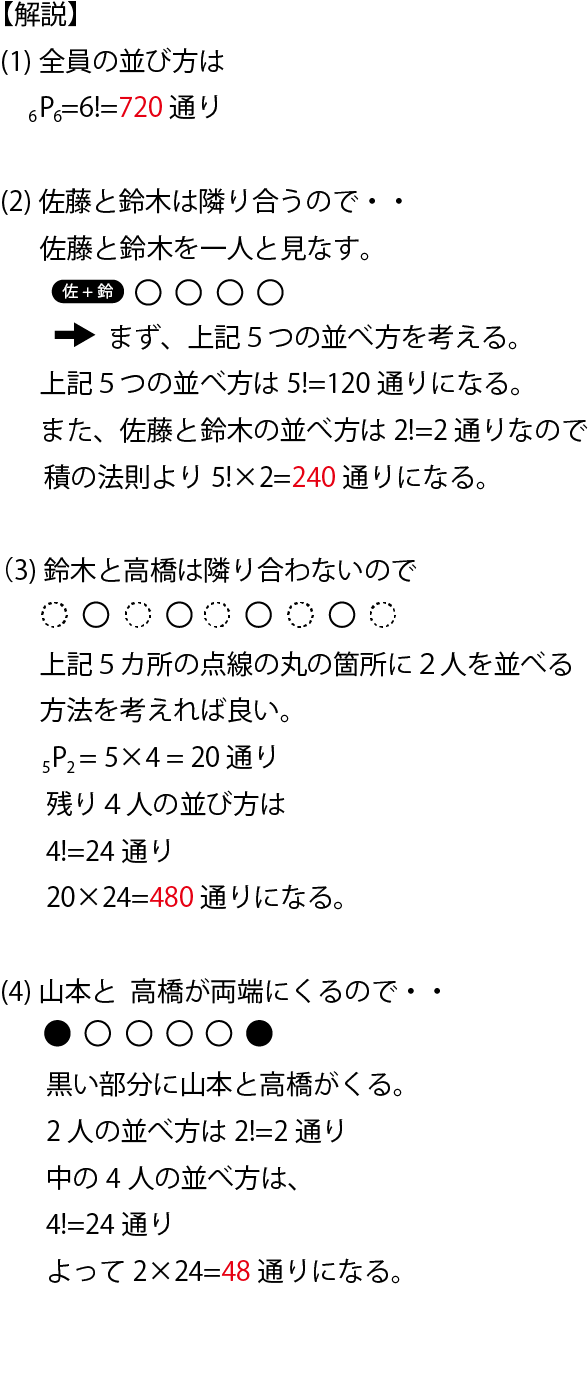
この26番の問題で 男子が少なくとも一人含まれるときは何通りかという問 Yahoo 知恵袋




場合の数 これだけは覚えよう 並べる と 選ぶ の計算方法の違い 中学受験ナビ



5人から3人選ぶ組み合わせは 何通りですか また 式と考え方もお願い Yahoo 知恵袋
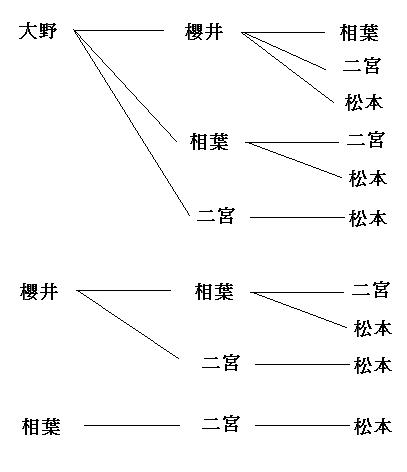



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




Combin関数で組み合わせの数を求める Excel関数 できるネット




ポーカーの確率 カードの組合せ総数と 各役の出現率
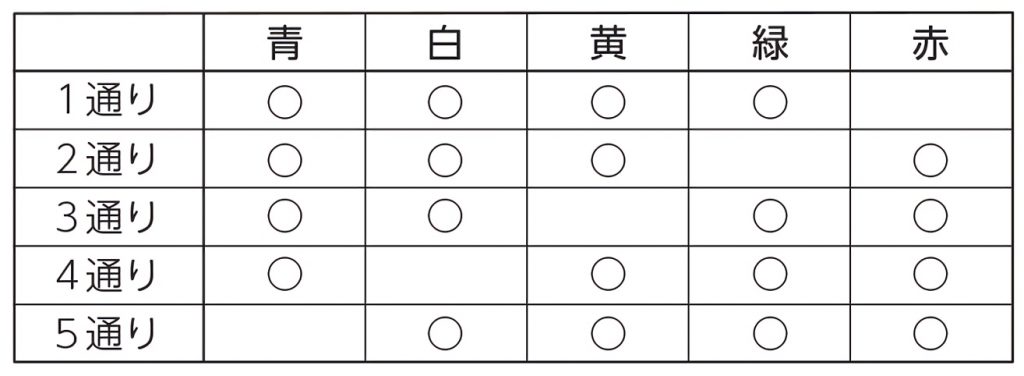



小6算数 場合の数 2 指導アイデア みんなの教育技術




5エン
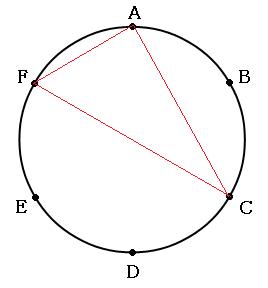



場合の数で解く図形問題の解き方を解説 図形問題かと思った 残念 場合の数でした
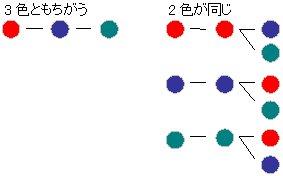



場合の数




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学a 重複組合せの基本 Nhr X Y Z の展開式の項の種類 受験の月
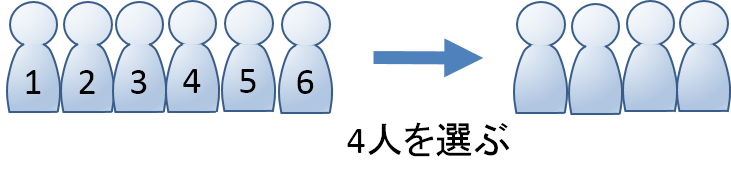



7 3 Cの使い方 統計学の時間 統計web
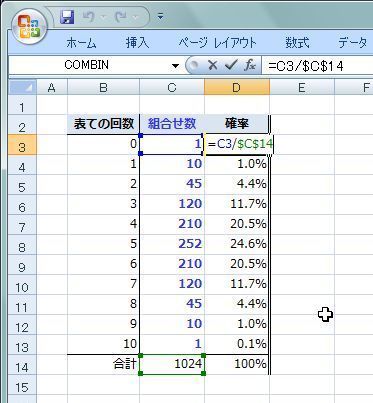



Combin関数で組合せ 抜取り の数を求めてみた Excel 数学関数 Haku1569 Excel でらくらく データ分析




4番の問題なんですけど答えは8通りなんですけど どうしてなのかわかりません Clearnote




Spi 数学 対策問題 組み合わせ 順列 しかくのいろは



算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素




赤玉 青玉 白玉が5個ずつ入った箱から5個の玉を取り出す 取り出し方の組み合 Clearnote



場合の数 組み合わせ 中学受験 田中貴 Com




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




ミニロトは何通りの組み合わせがある 全部の購入金額や当選確率と期待値を調査 気になルーキー調査隊



2



数字の組み合わせの問題で 7人の中から3人選ぶ組み合わせは何通りあるのでし Yahoo 知恵袋




組み合わせ C とは 公式や計算方法 は何通り 受験辞典




小6 算数 小6 40 並べ方 組み合わせ方 Youtube




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ
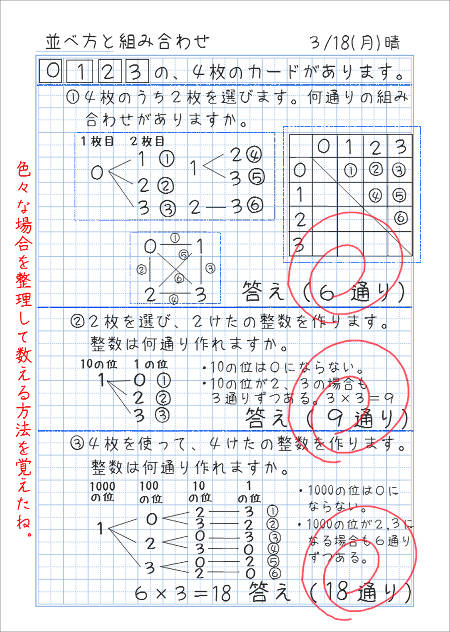



並べ方と組み合わせ方 その2 家庭学習レシピ



1
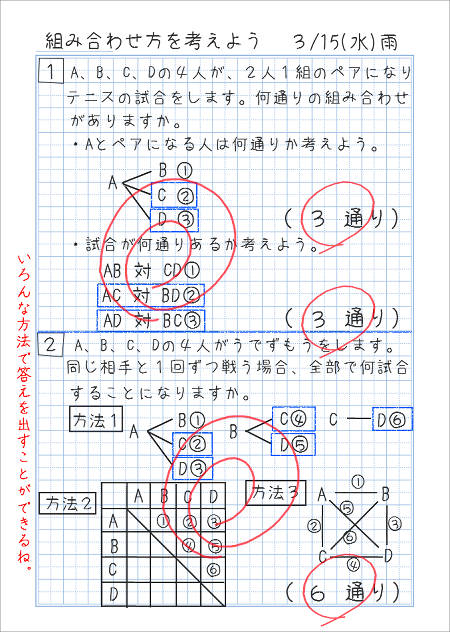



並べ方と組み合わせ方 その1 家庭学習レシピ




組合せは1時間で解けるようになる 外資系コンサルタントが主夫になったら



組み合わせの考え方と公式 組み分けと道順を求める問題の解き方
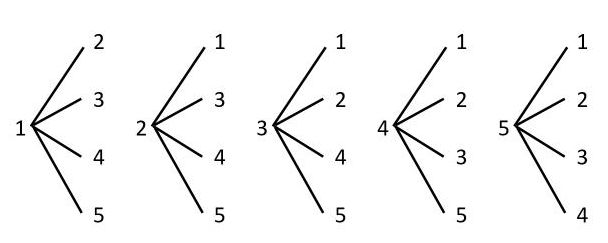



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




小6算数 ならべ方と組み合わせ方 学習プリント 練習問題 無料ダウンロード印刷




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



組み合わせ
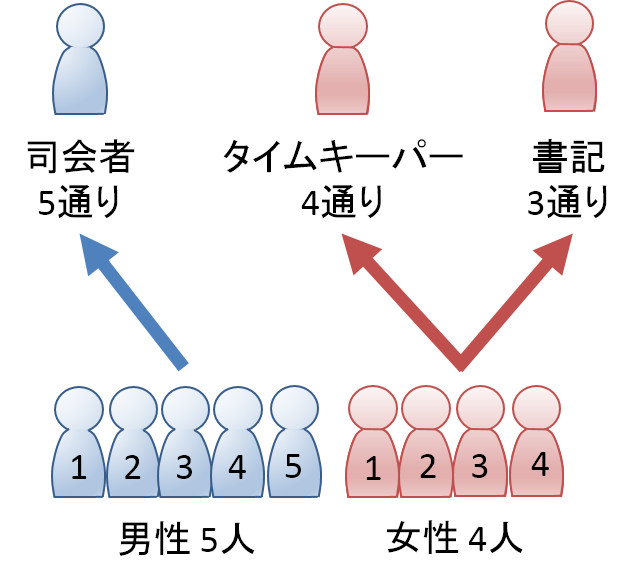



7 2 Pの使い方 統計学の時間 統計web




この問題の解き方を教えてください Clearnote




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
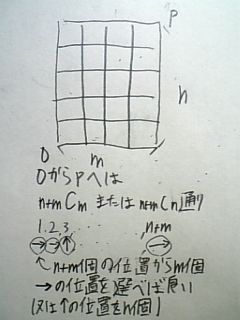



最短距離の道のりを進む方法は何通りあるか の解法 わんこら日記



確率の問題です A B C D Eの5人から3人の委員を選ぶとき 何 Yahoo 知恵袋




Combin関数で組合せ 抜取り の数を求めてみた Excel 数学関数 Haku1569 Excel でらくらく データ分析




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせ Alis




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ



場合の数 おやつランキングを予想しよう 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




高校数学 数a 15 組合せ 文字編 Youtube



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




場合の数 これだけは覚えよう 並べる と 選ぶ の計算方法の違い 中学受験ナビ
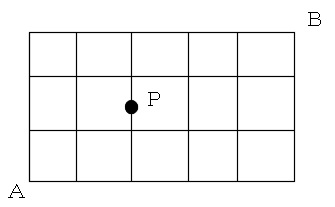



組み合わせの考え方と公式 組み分けと道順を求める問題の解き方




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ



順列と組み合わせの違いをリレーのチーム選考に例える コード7区



2



トランプの組み合わせは全部で何通りあるのか News Magic More



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



1




8月1日 小6算数 夏期講習 期 ジャングルジムブログ




場合の数 これだけは覚えよう 並べる と 選ぶ の計算方法の違い 中学受験ナビ



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




Win5全通り点数何通りでいくらになるか実践 競馬で勝つ方法 研究レポート うまめし Com 競馬必勝法



0 件のコメント:
コメントを投稿