場合の数と確率 kaztastudy 苦手な人向け組み合わせCの計算のやり方を簡単にサクッと解説するぞ! ツイート;組み合わせとは異なるn個の中から異なるr個を取り出す場合の数のことです。 例として、A、B、Cの3つの中から2つを取り出す場合を考えましょう。 書き出してみると、{AB}、{AC}、{BC}のように3通りで、 ポイントは順列と違い、ABとBAを同じものとして考えること です。※ この公式は,全部使う場合 の ※ もちろん, b の行き先の番号札3個をもらう方法の数 5 C 3 で計算しても同じになる. 5 C 3 = =10 《問題》 正しいものを選んでください. 選択肢をクリックすれば採点結果と解説が出ます.暗算では無理ですから計算用紙で計算してから答えてください. ≪1

場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん
場合の数 組み合わせ 中学
場合の数 組み合わせ 中学-が返されます。 組み合わせは、順序に意味がある順列とは異なります。 総数 = n、抜き取り数 = r とすると、組み合わせの総数は、次の数式で表されます。 問題3それぞれA,B,Cと書かれたカードがあります。この3Def cmb(n, r) if n r < r r = n r if r == 0 return 1 if r == 1 return n numerator = n r k 1 for k in range(r) denominator = k 1 for k in range(r) for p in range(2,r1) pivot = denominatorp



7 3 Cの使い方 統計学の時間 統計web
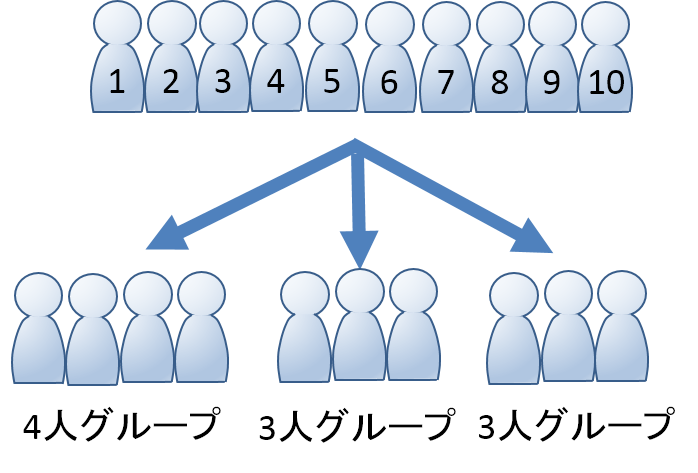
場合の数分野では,\ 断りがない限り,\ 人は区別できると考える よって,\ は{「モノの区別可」「組の区別可」「要素の個数固定」}型である これは,\ 組分けの中で最も基本的で単純な型である a君,\ b君,\ c君に,\ 順に3個ずつ{選}{ん}{で}分ける}と考える} まずそのため 確率を極めたければ,場合の数 場合の数の問題は大まかに分けると 順列 と 組み合わせ があり,これらは掛け算と割り算を駆使することで求めることができます. では実際に解いてみましょう! 1a,b,cの3人を1列に並べる方法は何通りあるか. *1 解答1 書き出す解き方 SPI 場合の数 順列・組み合わせの基礎 この単元の基礎は分量が多いです。 頑張って学習しましょう! ! 1 PとCの使い分けの解説です。 If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations
\( _5\mathrm{C}_2 \times _4\mathrm{C}_2\) 「場合の数」は公式自体は少ないですが問題のパターンが豊富です。 少し時間をかけて演習した方が良いと思いますよ。 ⇒ 場合の数 順列と組み合わせの違いと並べ方問題の解き方 順列の基本から確実に解いていきましょう。組み合わせの求め方 図や表を使うと、組み合わせを求めることができます。 例えば、下のような表や図で、5つのうち2つを選ぶ組み合わせを求めることができます。 表を使う の数が組み合わせ ※数えると10通りになる a a b b c c d d e e ※数えると10通りK, n C k, C n,k または C(n, k) のような記号で表す。ただし、この数は数学のあらゆる分野に頻繁に現れ、大抵の場合 () と書かれる。特に二項定理 () = = ()
今回の記事では高校数学Aで学習する 「組み合わせCの計算のやり方」 についてイチから解説していくよ。 この記事を通して、次のようなCの計算ができる数式ツールにて順列nPkや組み合わせnCkの記述の仕方がわかりません。 すなわち、左下と右下に添え字を書けられれば解決するのですが、どこを探してもそのような選択肢が出てきません。 これは仕様の問題なのでしょうか? どなたか教えてください。 12 組み合わせとは? 異なるn個の中から異なるr個とる 組み合わせ の数のことです。 5人(a、b、c、d、e)の中から2人を選ぶ組み合わせを考えましょう。 この時、{ab}、{cd}、{ac}のようになり、合計は10通りになります。ここでなぜ、順列の総数の半分になる




数学 Ncr 組み合わせ コンビネーションの計算方法と意味




7 3 Cの使い方 統計学の時間 統計web
3 4つのものの中から2つ選ぶ組み合わせと,その場合の数について考える。 T ちょっと待って。みんなから出た組み合わせは6通りだけど,もうほかにないのかな?3つの方法で考えてみよう。 ・まが玉式 ・ベース式 ・リーグ式 C やっぱり6通りだ。 組み合わせの数を落ちなく考える3つの方法を 場合の数③ 組み合わせ 例題5 a君、b君、c君、d君、の4人の中から、2人図書委員を選ぶとき、選び方は何通りあるか求めなさい。 解説 今までの問題とは違い、順番は関係ありません。例えばa君とb君の二人を選ぶとき「ab」と「ba」の違いは無いのです。 それを考慮して考えると、下のN n n 種類のものから重複を許して r r r 個選ぶ場合の数を n H r {}_n\mathrm{H}_r n H r と書くことがあります。 重複組合せの公式より n H r = n r − 1 C r {}_n\mathrm{H}_r={}_{nr1}\mathrm{C}_r n H r = n r − 1 C r です。 ただし,重複組合せの問題はさきほど述べた「仕切りの考え方」で必ず解けます。そのため



順列と組み合わせを計算する Permut Combin関数 Excel関数



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ
高校数学Aで学習する場合の数の単元から 「重複を許す組み合わせ」 について解説していきます。 重複を許す組み合わせとは次のような問題のこユーザ定義型3(評価 ☆☆) 「 組み合わせの数 」 にある方法をPythonで実装 samplepy Copied!ドからシまでの12個の半音から7つの音を選んだ場合何通り作れるか ご意見・ご感想 792通りで思ったより多かった 9 1131 歳代 / エンジニア / 役に立った / 使用目的 導入の検討をしている顔認識ツールに対する性能評価のため。 nC2としたとき十分な組み合わせの数が得られるものを



順列 組合せ 確率 統計 web教材 木暮
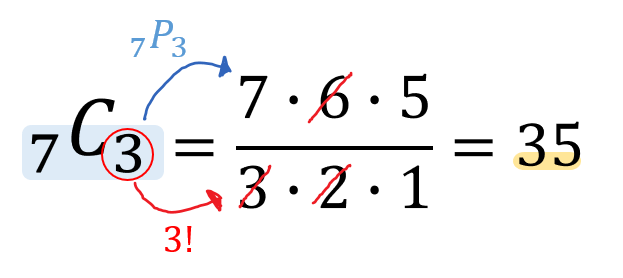



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ
場合の数 | 順列(P)と組合せ(C)の違いは?どう使い分ける? 場合の数と確率 Photo by Anastasiya Romanova on Twitter Facebook はてブ Pocket LINE コピー 今回は、順列と組合せについて解説します。 第1章から第3章までは、順列(P)と組合せ(C)について、意味や計算の仕方に組合せ数学(くみあわせすうがく、英語 combinatorics )あるいは組合せ論(くみあわせろん)とは、特定の条件を満たす(普通は有限の)対象からなる集まりを研究する数学の分野。 離散数学の中核の一つとされる。特に問題とされることとして、集合に入っている対象を数えたり(数え上げ的総数 < 0、抜き取り数 < 0、または総数 < 抜き取り数である場合、エラー値 #NUM!



重複組合せ



場合の数 確率を体系的に学ぼう 教科書でバラバラに登場するパターンを整理して把握しよう オンライン受講 東大に 完全 特化 東大合格 敬天塾
実際に出会う問題では、積の法則や和の法則を単独で用いることは少なく、これらを組み合わせて使います。 そのとき、場合分けした「各々の場合を積の法則で処理し」「全体を和の法則でまとめる」という流れが基本です。 例1 3つのさいころ a 、 b 、 c を同時に投げるとき、出た目の和場合の数・組み合わせ(1) の数が組み合わせ ※数えると10通りになる A A B B C C D D E E ※数えると10通りになる 頂点どうしを結ぶ 線の数が組み合わせ 図を使う A C D B E Title kumiawase01 Created Date 2/5/13 AMC言語で使用する標準関数、アルゴリズムなどのサンプルプログラムを掲載しています。 C言語例 を掲載しています。 C言語例文集 場合の数 (順列、組合せ、重複組合せ) 高校数学で勉強する順列(Permutation)、組合せ(Combination)、重複組合せ(Homogeneous product)を求めるプログラ




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




1 順列と組み合わせについて 数学帝國への逆襲 西春自習質問教室のブログ
この場合、 5勝0敗になる組み合わせ=5C5=1通り 4勝1敗になる組み合わせ=5C4=5通り 3勝2敗になる組み合わせ=5C3=10通り ・・・ では、0勝5敗になる組み合わせは? 5C0=1通りですね。 11人がナイス!しています ナイス! 質問者からのお礼コメント 補足までありがとうございます!! お礼場合の数と確率 順列pと組み合わせcの違いと"簡単"な見分け方 21年8月9日 「順列と組み合わせの意味が分からない」 「順列と組み合わせの見分け方を教えて」 今回はこんな悩みを解決します。 高校生 順列と組み合わせの使い分けがよく分からないんだよ さっそくですが1つ質問をします①a,b,cの区別を無くした場合になぜ、同じものとなる分け方がa,b,cの順列の総数の3!になるのかがわかりません。 ②なぜ、a,b,cの区別したものを、A,B,Cの順列の総数で割るのかもわかりません。 ①は図つきで説明してもらえると、大変助かります。 進研ゼミからの回答! こんにちは




組み合わせcの公式と使い方を徹底解説 5分でサクッと解説




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら
場合の数 高校の時の「 3 P 2 」とか「 3 C 2 」を覚えてますか? 公式はとてもカンタンなので、 完全に忘れていても30秒で覚えられます。 忘れている方 ⇒ 最速解法と例題 覚えている方は腕試し! ⇒ 問題11(組み合わせ)道順の場合の数を求める別解を解説します。「書き込み方式」などと呼ばれるものです。 点 a a a から頂点 p p p にたどりつくための最短の道順の数を n (p) n(p) n (p) と書きます。目標は n (b) n(b) n (b) を求めることです。Top spi非言語 場合の数 問題11(組み合わせ) 今回はじめて タグ青 タグ黄 タグ赤 タグ白 3 分 制限時間 1 00 非表示 表示 問題 あるサークルには、男性6人と女性4人が所属している。この中から掃除当番を4人選びたい。 (1) 男性だけから4人選ぶとすると、選び方は何通りあるか。 選択




高校数学 数a 17 組合せ 道順編 Youtube




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
場合の数と確率 / 場合の数/順列/ 順列と何が違うかというと、順列の場合は「順番をつける」、組み合わせの場合 は「順番をつけない」この違いなんですね。 10色のカラーボールから4色のボールを選ぶ方法は何通りあるか考えてみましょう。 これは典型的な組み合わせの問題です。異なるn ② 左から順にそれぞれの枠に入れる場合の数を考える。 ③ 連続して起こっているので、かけ算をして求める。 組合せの求め方 例題2の「5文字から3文字を選ぶ」のように、選ぶだけを組合せという。 求め方は、組合せの公式Cを用いて解く。 例えば、 このように計算する。 例題1場合の数前回 https//wwwyoutubecom/watch?v=tpOLtMx_Bfk 次回 https//wwwyoutubecom/watch?v=pq3pJVNZrIU&index=15&list=PLKRhhk0lEyzPV58dAXzmfZle_wg03CLhl




組み合わせ C とは 公式や計算方法 は何通り 受験辞典




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら
組み合わせ C とは?公式や計算方法( は何通り?) 順列と組み合わせの見分け方例題 人を選ぶ場合の数は \({}_7 \mathrm{C}_3 = \displaystyle \frac{7 \cdot 6 \cdot 5}{3 \cdot 2 \cdot 1} = 35\) よって、男子 \(2\) 人、女子 \(3\) 人の \(5\) 人を選ぶ場合の数は \(28 \times 35 = 980\) 答え: \(980\) 通り (2) 男子は A重複組み合わせの数 桜花学園大学教授 岩井 齊良 異なる n 個のものから重複を許して r 個のものを取り出す場合の数 n H r は,公式 n H r = nr1 C r によって求められる。この公式を説明しよう. 自動販売機による説明 次のようなジュースの販売機があるとする. それぞれの図柄のボタンを しかし、組み合わせなので1,2と2,1のように 重複する組み合わせのペアを1通り と数える必要があります。 よって、組み合わせの総数は\12 \div 2 = 6 \となり、6通りとなります。 (3) 組み合わせの記号 C




Cとpって何が違うんですか Clear




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート
場合の数と確率 kaztastudy 重複を許す組み合わせHを使った公式、仕切りを使った考え方を解説! ツイート;場合の数5|同じものを含むと順列の場合の数はどう変わる? 場合の数6|重複組み合わせは2パターンでok! 場合の数7|二項定理を理解しよう!場合の数を使って導出! 場合の数8|展開が楽にできる「パスカルの三角形」の考え方 Cは組み合わせの場合の数を求めるときに使います。 Pと少し違う部分がありますが、先に式を書きます。 $${}_n C_k=\frac {n!}{( nk) !( k!) }$$ 一見複雑に見えますが、先ほどからやっている事を思い出してみれば簡単です。 6個の中から2個取り出して、列には並べないので重複する部分が




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




高校数学a 組合せの活用2 男女の選び方 例題編 映像授業のtry It トライイット




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生
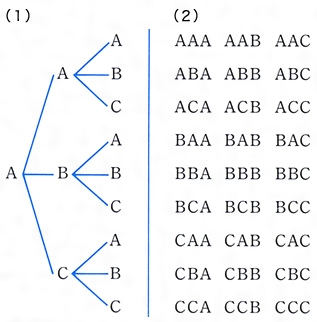



場合の数とは コトバンク



3
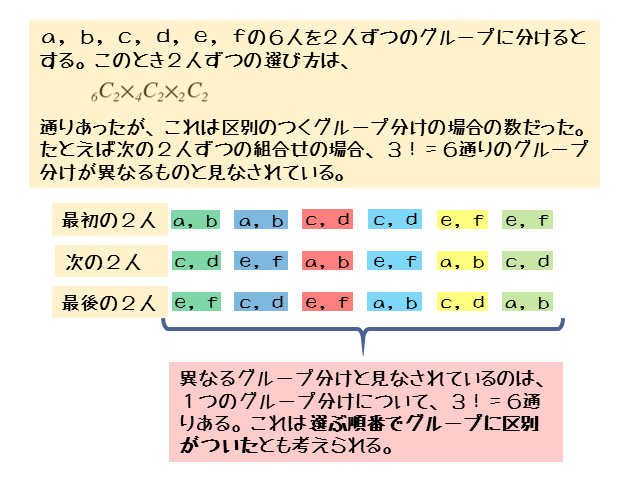



場合の数 グループ分けについて 日々是鍛錬 ひびこれたんれん




高校 数学a 場合の数31 pとcの違い 11分 Youtube




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



確率基礎問題 Of 京極一樹の数学塾会員頁




順列pと組み合わせcの違いと 簡単 な見分け方




苦手でも分かる 順列 P と組み合わせ C の使い分け 確率 ともよし塾 受験と科学の解説授業




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長




高校数学a 同じものを含む順列 N P Q R 受験の月




高校数学a 重複組合せ Nhr 受験の月



1
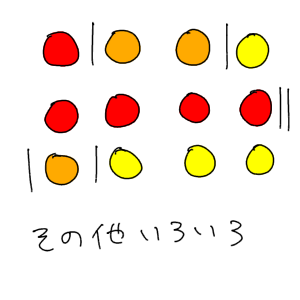



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート
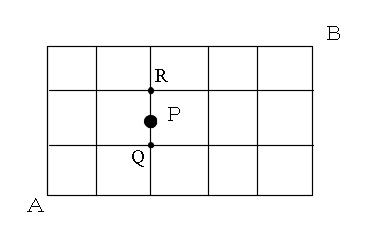



組み合わせの考え方と公式 組み分けと道順を求める問題の解き方




順列と組み合わせ 算数用語集




高校数a 場合の数 Cの計算方法 オンライン無料塾 ターンナップ Youtube




場合の数 並べる と 選ぶ の計算方法の違い




苦手でも分かる 順列 P と組み合わせ C の使い分け 確率 ともよし塾 受験と科学の解説授業




スマホok 6年 並べ方と組み合わせ方 場合の数 並べ方を考えよう Youtube




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



1




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ
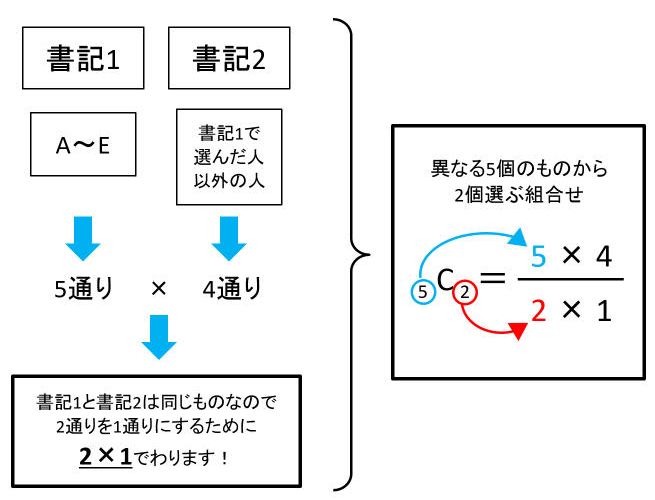



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 ページ 2 2 中学受験ナビ




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説




順列pと組み合わせcの違いと 簡単 な見分け方
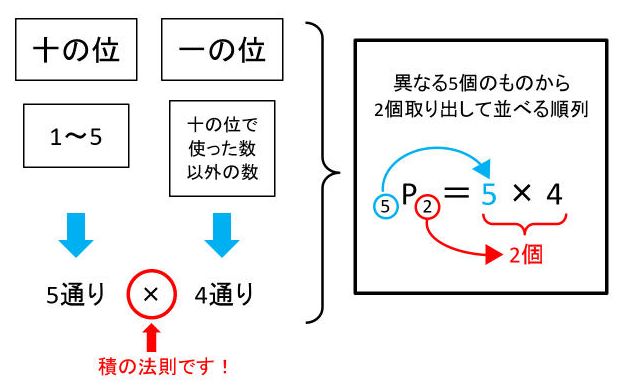



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




場合の数 番外編 順列p 組合せc 教遊者



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




場合の数 組み合わせの計算方法について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
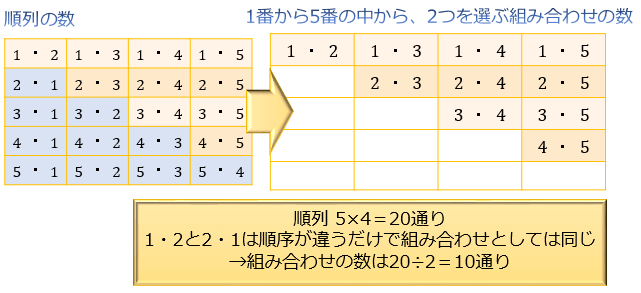



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




場合の数 無料で使える中学学習プリント
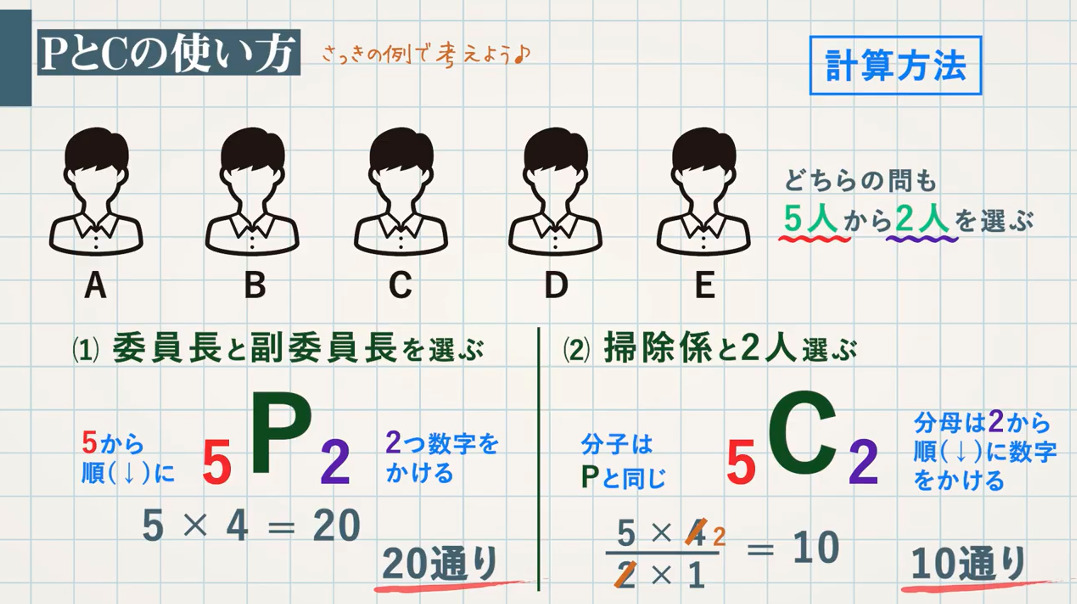



場合の数 番外編 順列p 組合せc 教遊者




中学数学 場合の数
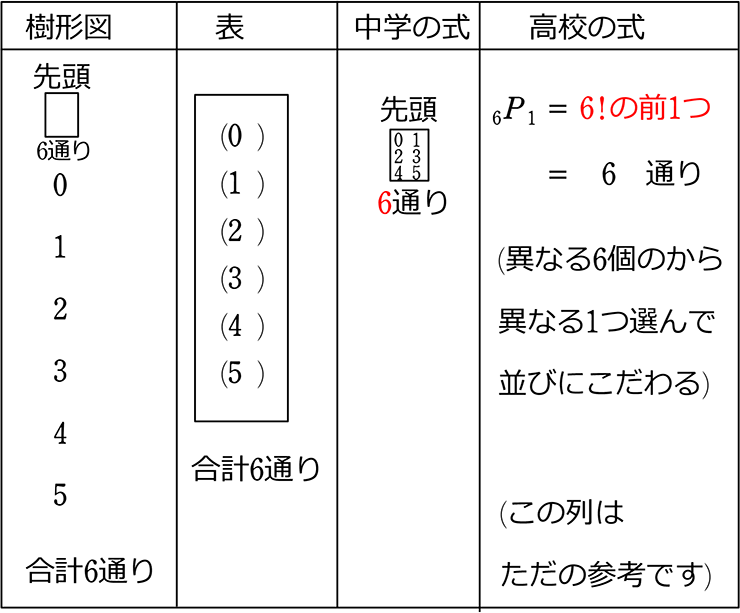



中学数学 場合の数




場合の数36 重複組合せの導入1 怜悧玲瓏 高校数学を天空から俯瞰する




5分で分かる 確率統計 Ncr の計算方法 あぱーブログ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




場合の数 番外編 順列p 組合せc 教遊者




順列と組み合わせの公式とその違い 問題付き 理系ラボ




高校数学 数a 14 組み合わせ 基本編 Youtube




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




高校数学a 組合せとは 映像授業のtry It トライイット




高校数学a 組合せの基本と順列との関係 Ncrの性質 受験の月



9 3 確率の計算 順列 組み合わせ 統計学の時間 統計web




5講 組合わせ 1章 場合の数と確率 問題集 高校数学a



中学受験対策11 場合の数 攻略法 さんすうがく




場合の数 並べる と 選ぶ の計算方法の違い




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




数探高校講座 数学a 場合の数と確率 5 組合せ 数学探究所




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




リーグ戦とトーナメント戦 小学校6年教材より 身勝手な主張
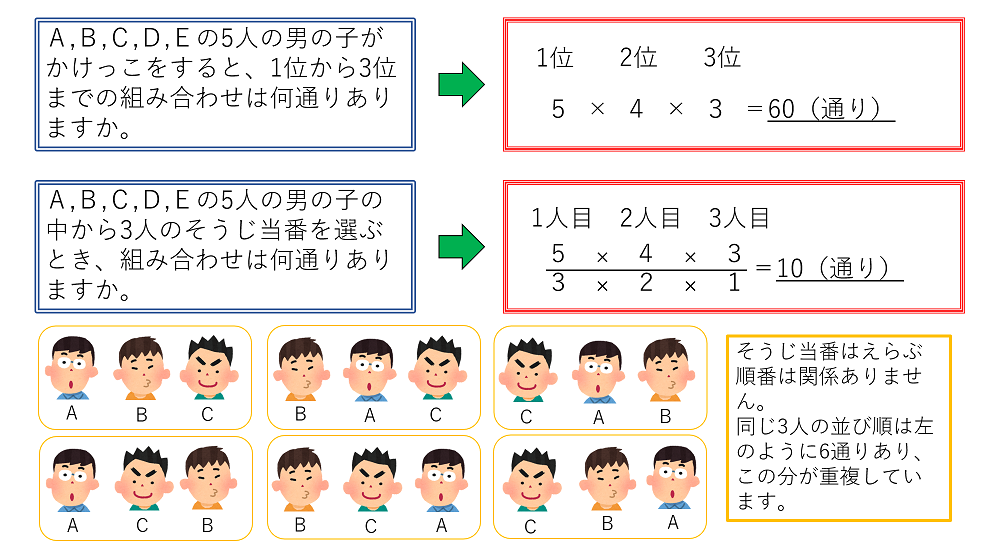



上何 通り ある か 計算 小学生 子供のための最高のぬりえ
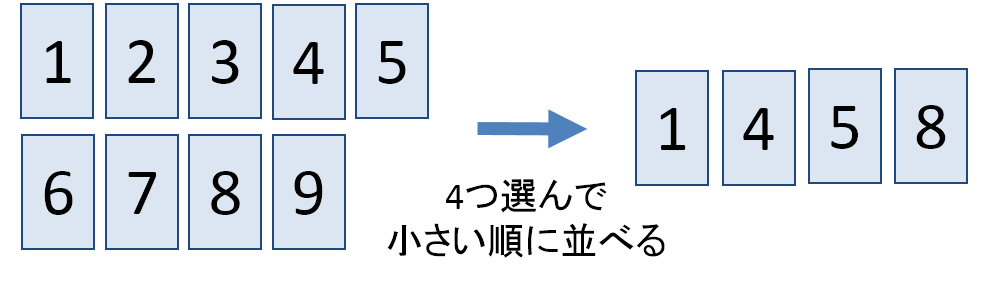



7 3 Cの使い方 統計学の時間 統計web
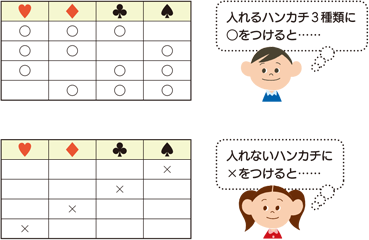



順列と組み合わせ 算数用語集




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
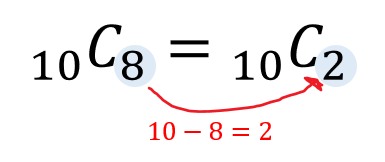



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




場合の数39 重複組合せで楽になるいいかえ 怜悧玲瓏 高校数学を天空から俯瞰する



1




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




高校数学a 場合の数 順列と組合せ 階乗 とc 組合せ を使いこなそう Clear
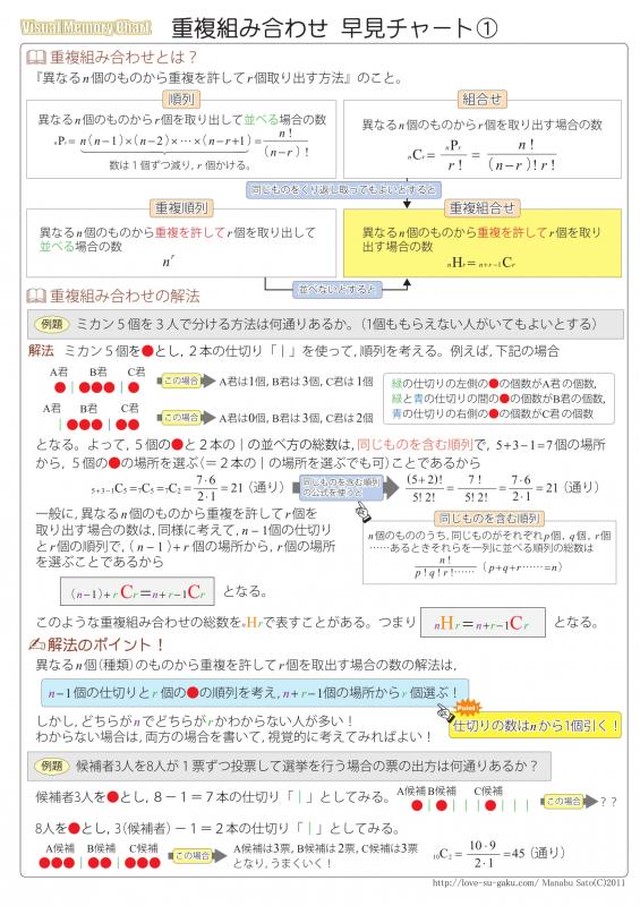



数学a 重複組み合わせ問題 場合の数 チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru




順列と組み合わせの公式とその違い 問題付き 理系ラボ



重複組合せの考え方 思考力を鍛える数学




順列の問題 一定の条件で並べる 高校数学の知識庫




高校数学a Npr と Ncr の使い分け 練習編 映像授業のtry It トライイット
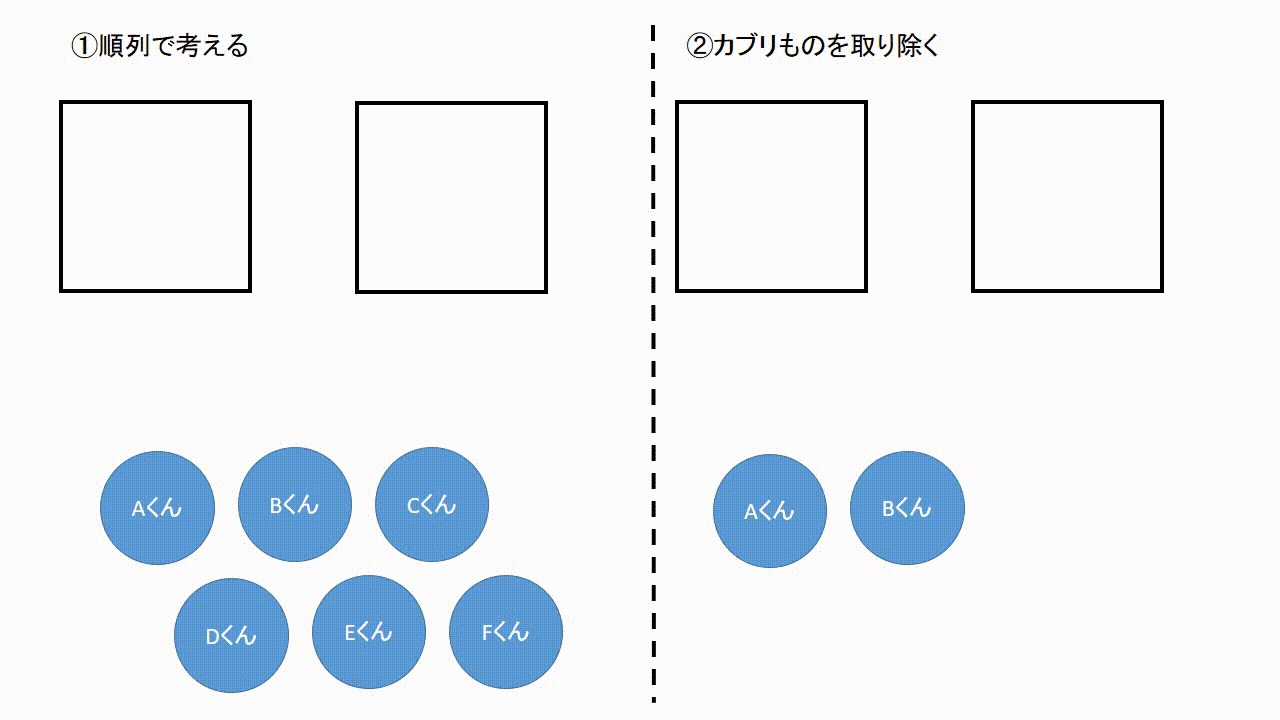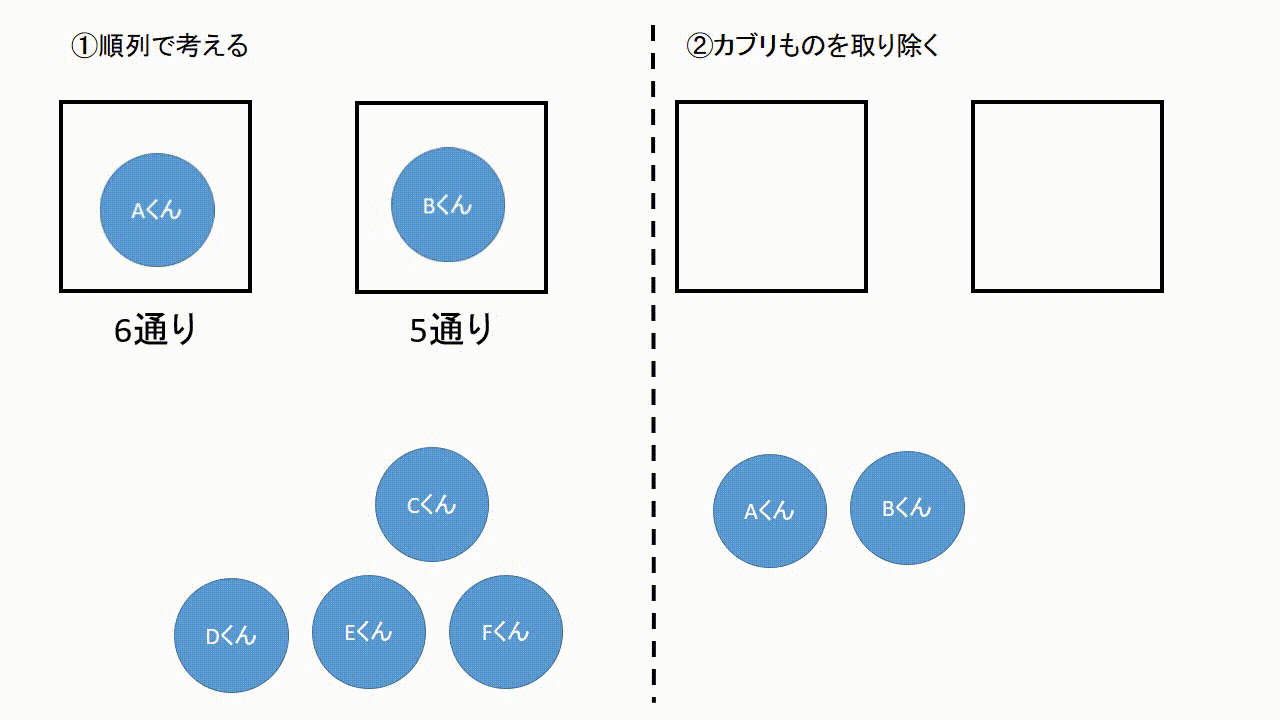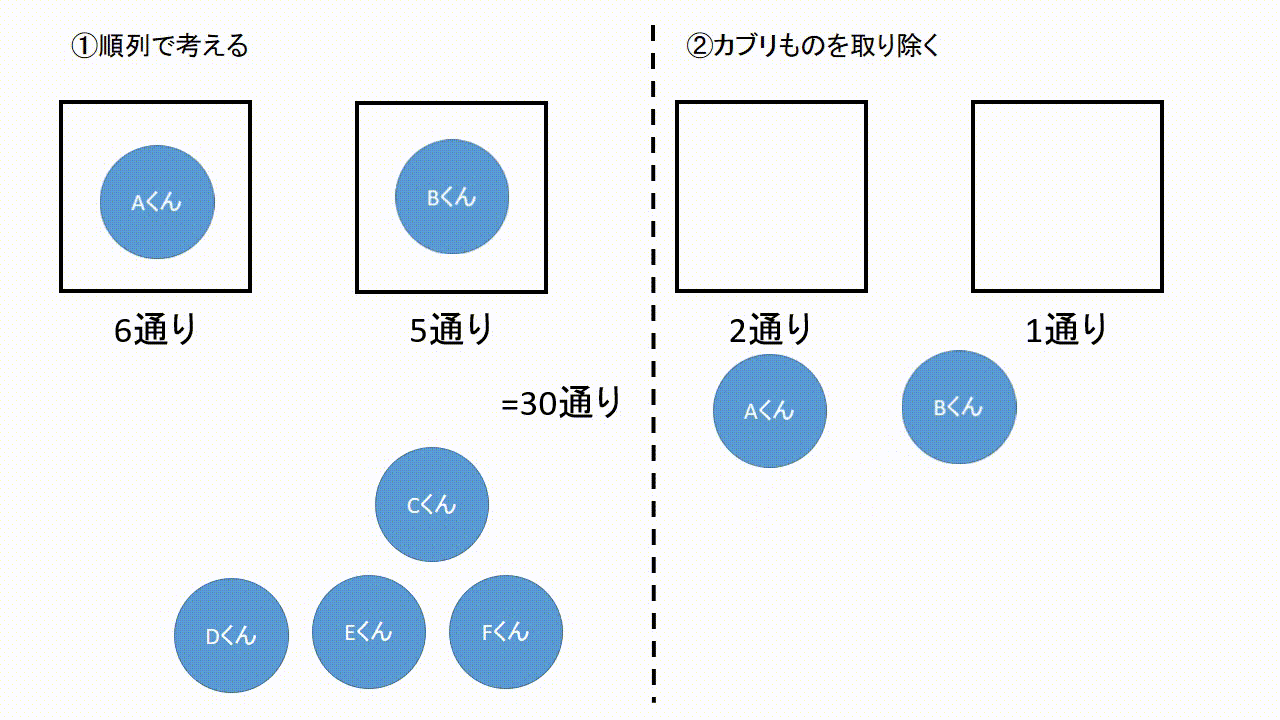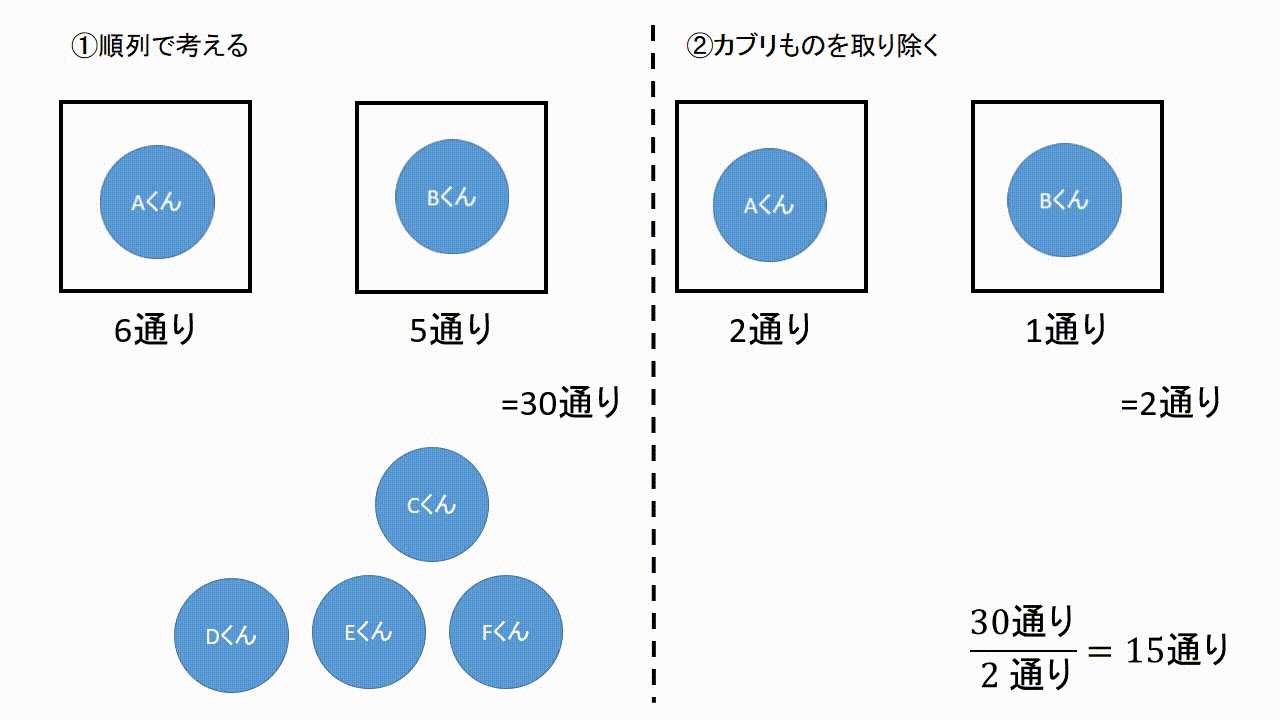



数学 確率を極めるには 場合の数 を極めろ




5講 組合わせ 1章 場合の数と確率 問題集 高校数学a



場合の数と確率を総まとめ 各種公式 重要記事一覧 受験辞典




重複順列と重複組合せ 感じる科学 味わう数学
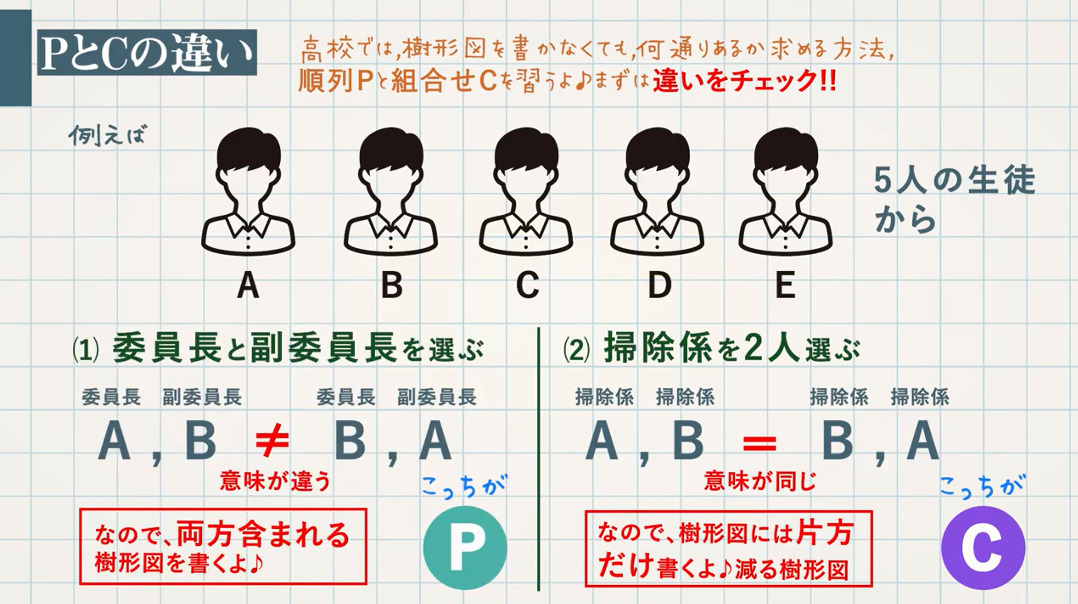



場合の数 番外編 順列p 組合せc 教遊者



0 件のコメント:
コメントを投稿